We study how topology is revealed, fluctuates, and disappears in topological materials under disorder. Using space-resolved topological markers, we show that topological phase can be described by local order parameters with meaningful fluctuations and correlations. Large-scale simulations of disordered two-dimensional topological insulators demonstrate that short-range fluctuations average out under coarse graining, except at disorder-driven phase transitions where correlations become long-ranged. Near these critical points, universal scaling laws and growing correlation lengths emerge, distinguishing different topological transitions. In this [Phys. Rev. Lett. 135, 026603 (2025)] we connect topological phases with the language of critical phenomena and real-space order. See also SISSA's press release on [Topological materials and critical phenomena: the unexpected connection between two worlds].
Electronic-Structure Theory & Methods
Theory and simulation of non-crystalline topological phases
Non-collinear Koopmans spectral functionals
The presence of spin-orbit coupling or non-collinear magnetic spin states can have important effects on materials properties, in particular on excited states. Together with Nicola Colonna (PSI), we have developed non-collinear Koopmans-compliant functionals based on Wannier functions and density-functional perturbation theory (see [Physical Review Research 6 (3), 033085 (2024)]); these are functionals of four-component orbitals densities that can be obtained from the charge and spin-vector densities of Wannier functions. The predicted band gaps are very accurate, also for technology-relevant materials such as III-IV semiconductors and perovskites, and include spin-dependent interactions and screening effects that are not accounted for in standard diagrammatic approaches based on the random phase approximation.
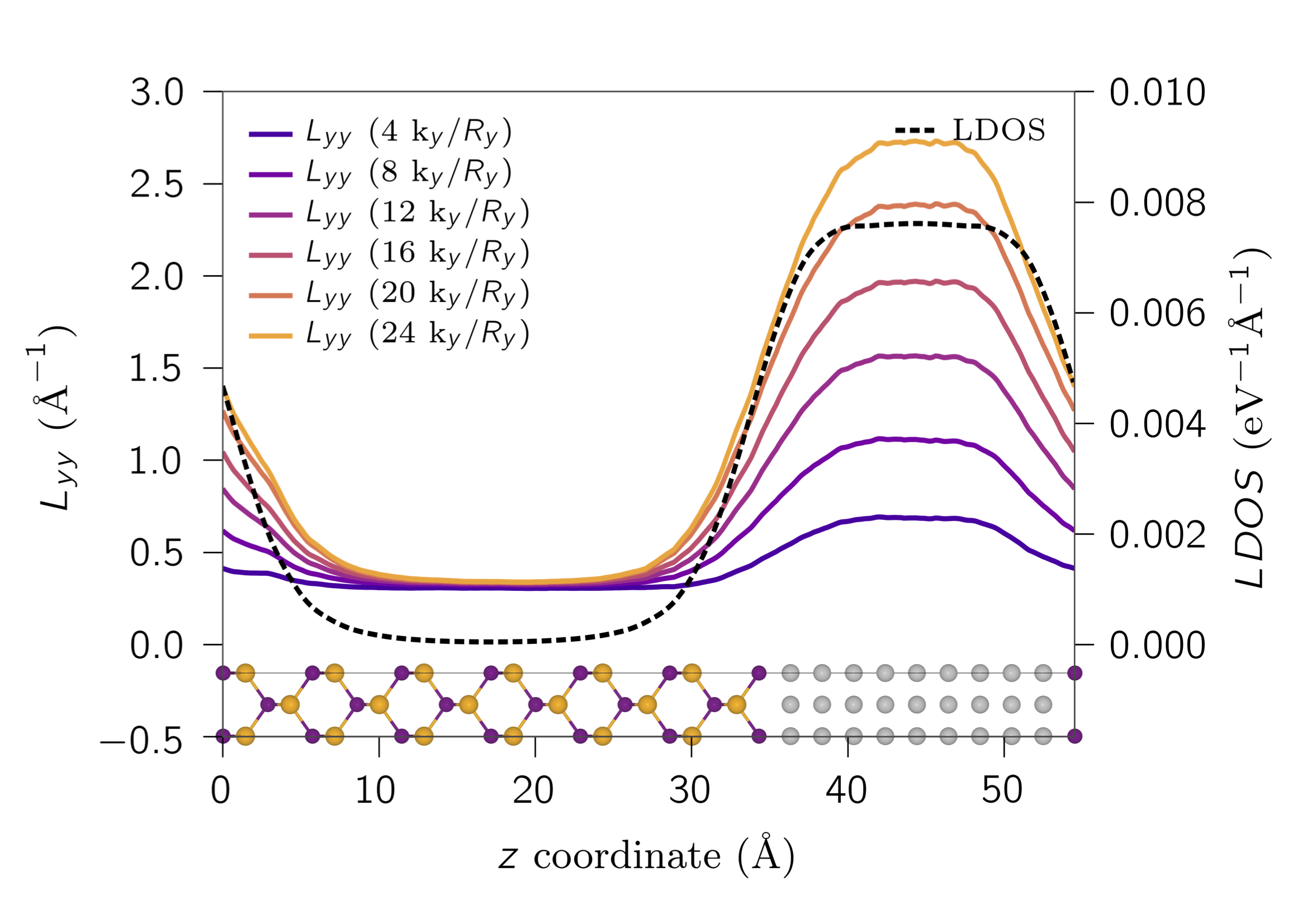
Locality of geometrical and topological properties of the electronic structure
Several properties in electronic-structure theory are defined as geometrical and topological quantities in reciprocal space, such as the Berry curvature or the quantum metric. Among these quantities we find topological invariants, the anomalous Hall conductivity, orbital magnetization and many others. I have been developing local counterparts for a few geometrical properties of the electronic structure, both for tight-binding and first-principle calculations.
For example, together with Raffaele Resta I have been showing that the orbital magnetisation of a magnetic metal does not depend on the boundary [Phys. Rev. Lett. 116, 137201 (2016)], contrary to the picture based on surface currents that is still present in most textbooks. Also the intrinsic part of the anomalous Hall conductivity is a local quantity [Phys. Rev. B 95, 121114(R) (2017)] both in insulators and metals. We have also developed a local theory of the insulating state [Phys. Rev. Lett. 122, 166602 (2019)] that is solely based on the electronic ground-state.